- POJ 1416 - Shredding Company
- Time: 1000MS
- Memory: 10000K
- 难度: 初级
- 分类: 搜索
问题描述
公司现在要发明一种新的碎纸机,要求新的碎纸机能够把纸条上的数字切成最接近而不超过 target 值。
比如,target 的值是 50,而纸条上的数字是 12346,应该把数字切成四部分,分别是 1、2、34、6。因为这样所得到的和 43 = (1 + 2 + 34 + 6) 是所有可能中最接近而不超过 50 的(比如 1, 23, 4, 和 6 就不可以,因为它们的和不如 43 接近 50,而 12, 34, 6 也不可以,因为它们的和超过 50 了)。
碎纸还有以下三个要求:
- 如果 target 的值等于纸条上的值,则不能切。
- 如果没有办法把纸条上的数字切成小于 target,则输出 error。如 target 是 1 而纸条上的数字是 123,则无论你如何切得到的和都比 1 大。
- 如果有超过一种以上的切法得到最佳值,则输出 rejected。如 target 为 15,纸条上的数字是 111,则有以下两种切法 11、1 或者 1、11.
你的任务是编写程序对数字进行划分以达到最佳值。
解题思路
用 DFS 深搜:
- 比如一个 6 位数 n,切成为 6 个数的话,这 6 个数的和如果大于目标数 aim 则不用再搜索了,因为这肯定是所有划分中和最小的,而最小都比目标数大,自然就没有合要求的答案了.
- 如何切分,假如以 50 和 12346 为例:
- 第一步,先切下一个 “1”,然后递归去切 “2346”;
- 第二步,再切下一个 “12”,然后递归去切 “346”;
- 第三步,再切下一个 “123”,然后递归去切 “46”;
- 第四步,再切下一个 “1234” 然后递归去切 “6”
- 第五步,再切下 “12346”。
- 切下来的 前面的数字串部分 则加入到划分的和,剩下的部分继续递归,直到剩下的数字串长度为 0。 可以用一个 int 记录划分方式
(int p), 如上例的输入为 50 和 12346 时,其结果为43 = (1 + 2 + 34 + 6),那么p=1121,代表把 12346 划分为 4 部分,第一部分为第 1 位,第二部分为第 2 位,第三部分为第 3、4 位,第四部分为第 5 位 - 注意在搜索时,必须把 n 的 剩余数字部分 转化为字符串再搜索,不然若 剩余的数字开头第一位为 0 时,会导致出错。
- 剪枝方法:在搜索时若发现部分和 大于(不能等于)aim 时,则可结束搜索。
- error 的判定要在搜索前进行,rejected(多个最优解)的判定要在搜索后判定。
- 关于出现相同最优解的标记,每出每种划分的 sum 每出现一次标记 +1,要使标记为
O(1),只需把 vist 数组开得足够大。N 最多为 6 位数,因此Maxsum=999999
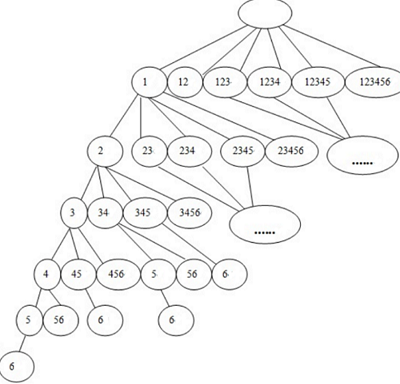
简单的附上一个关于例 50 和 12346 的不完全搜索树
省略号为未列出的结点
AC 源码
//Memory Time
//4160K 157MS
#include<iostream>
#include<cmath>
#include<string>
using namespace std;
int getlen(int n) //得到n的位长度
{
if(n<10)
return 1;
else if(n<100)
return 2;
else if(n<1000)
return 3;
else if(n<10000)
return 4;
else if(n<100000)
return 5;
else
return 6;
}
int getvalue(char* s,int i) //得到数字字符串s前i位字符(数字)组成的int值
{
int k=i;
int sum=0;
while(k)
{
k--;
sum+=(s[k]-'0')*(int)pow(10.0,(double)(i-k-1));
}
return sum;
}
int gethead(int n,int i) //得到由n的前i位数字构成的int
{
int len=getlen(n);
if(len<=i)
return n;
return n/(int)pow(10.0,(double)(len-i));
}
int gettail(int n,int i) //得到由n的后i位数字构成的int
{
return n%(int)pow(10.0,(double)i);
}
int aim; //目标数
int result; //最优划分的和
int path; //最优划分的划分方式
int sum; //某种划分的和
int p; //某种划分方式
int vist[1000000]; //记录每个sum出现的次数
//999999是当n=999999时的最大和值
void DFS(char* s,int len)
{
if(len==0)
{
vist[sum]++;
if(sum>result && sum<=aim)
{
result=sum;
path=p;
}
return;
}
for(int i=1;i<=len;i++)
{
int a=getvalue(s,i); //n的前i位字符转变为数字留下,计入部分和
sum+=a; //部分和
if(sum>aim) //剪枝,部分和已经大于aim,无需继续往下搜索
{
sum-=a;
continue;
}
p=p*10+i; //记录划分方式
char b[7]; //构造n的后i位字符序列,继续递归
int j=0;
for(int k=i;k<len;k++)
b[j++]=s[k];
b[j]='\0';
DFS(b,len-i);
sum-=a; //回溯
p/=10;
}
return;
}
int main(void)
{
while(true)
{
/*Input*/
char s[7]; //打印纸上的数字
cin>>aim>>s;
int len=strlen(s);
int n=getvalue(s,len); //构造s的数字序列n
if(!aim && !n)
break;
if(aim==n) //目标值与打印纸上的数字一致
{
cout<<aim<<' '<<n<<endl;
continue;
}
int num=n; //temporary
int k=0; //n的各位数字之和
while(num)
{
k+=num%10; //逐位划分是 和最小的划分方式
num/=10;
}
if(k>aim) //最小和也大于aim,则所有划分都大于aim
{
cout<<"error"<<endl;
continue;
}
/*Initial*/
result=-1;
sum=0;
path=0;
p=0;
memset(vist,0,sizeof(vist));
/*DFS*/
DFS(s,len);
/*Output*/
if(vist[result]>1) //最优解多于一个
cout<<"rejected"<<endl;
else if(vist[result]==1) //有唯一最优解
{
cout<<result<<' ';
int L=getlen(path); //输出划分的方式
for(int i=1;i<=L;i++)
{
int k=gethead(path,1); //取path的第一位k,k的值等于n的第一段划分位数,即从n的第1位到第k位
cout<<gethead(n,k)<<' ';
n=gettail(n,len-=k);
path=gettail(path,L-i);
}
cout<<endl;
}
}
return 0;
}



