- POJ 3414 - Pots
- Time: 1000MS
- Memory: 65536K
- 难度: 初级
- 分类: BFS
问题描述
给出了两个瓶子的容量A,B, 以及一个目标水量C,
对A、B可以有如下操作:
- FILL(i): fill the pot i (1 ≤ i ≤ 2) from the tap;
- DROP(i): empty the pot i to the drain;
- POUR(i,j): pour from pot i to pot j; after this operation either the pot j is full (and there may be some water left in the pot i), or the pot i is empty (and all its contents have been moved to the pot j).
问经过哪几个操作后能使得任意一个瓶子的残余水量为C。
若不可能得到则输出impossible
解题思路
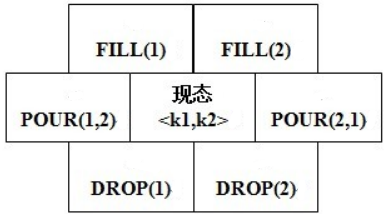
6入口的BFS
把两个两个桶的某个同一时间的状态看做一个整体,视为初态
可对初态进行六种操作,即 FILL(1), FILL(2), DROP(1), DROP(2), POUR(1,2), POUR(2,1)
这6种操作在我的程序中分别用一个整数进行记录:
- 1z0: 清空z瓶子
- 2z0: 装满z瓶子
- 3xy: 从x瓶倒向y瓶
x,y,z∈{1,2}
这样在输出操作时就能根据数字的特点 进行选择性输出 了
这题有两个难点
第一就是要输出得到容量C的过程:
对于BFS的题而言这种要求是非常刁钻的,回溯每一步时很容易就混淆了下标。
解决方法:对于每一步的操作,我们都得对它设置一个pos指针,使它指向前一步操作在 queue[] 队列的下标,即对下标进行回溯,再顺序输出每一步操作。
第二就是状态记录:
怎样记录两个瓶子在同一时间点的状态,又能使得搜索标记时为O(1)的复杂度?
瓶子某时刻的残余水量就是该瓶子的状态,设残余水量为k1 k2
开始时我想对k1 k2进行各种运算组合,但都无法保证k1 k2的运算组合是独一无二的。
最后我决定用 ostringstream 在k1 k2 两个数字之间加上一个逗号,把他们变为字符串string,再利用map进行标记,相当成功。
最后我简单说说各种操作的数学表达式:
设1瓶的容量为v1,残余水量为k1, 2瓶的容量为v2,残余水量为 k2 , 那么:
fill(1)相当于k1=v1fill(2)相当于k2=v2drop(1)相当于k1=0drop(2)相当于k2=0- 对于
Pour(1,2):
若k1+k2<=v2,则k2=k1+k2,k1=0(有先后顺序)
否则k1=k1+k2-v2,k2=v2(有先后顺序) Pour(2,1)亦同理
AC 源码
//Memory Time
//232K 32MS
#include<iostream>
#include<string>
#include<sstream>
#include<map>
using namespace std;
int v1,v2; //两个瓶子的容量
int c; //目标残余水量
int k1,k2; //在某状态时两个瓶子的剩余水量,temporary
typedef class
{
public:
int x,y; //当前状态(两个瓶子中的水量)
int pos; //记录前一状态在队列queue中的下标
int step; //当前步数
}process;
//把整数a、b整合为 "a,b" 的字符串形式(不包括引号),用于标记状态
string combAB(int a,int b)
{
string s;
ostringstream oss;
oss<<a;
oss<<',';
oss<<b;
s=oss.str();
oss.str(""); //清空oss对象内所存储的流
return s;
}
void fill(int i)
{
switch(i)
{
case 1: {k1=v1; return;}
case 2: {k2=v2; return;}
}
}
void drop(int i)
{
switch(i)
{
case 1: {k1=0; return;}
case 2: {k2=0; return;}
}
}
void pour(int i,int j)
{
switch(i)
{
case 1: // v1 to v2
{
if(k1+k2<=v2)
{
k2=k1+k2;
k1=0;
}
else
{
k1=k1+k2-v2;
k2=v2;
}
return;
}
case 2: // v2 to v1
{
if(k1+k2<=v1)
{
k1=k1+k2;
k2=0;
}
else
{
k2=k1+k2-v1;
k1=v1;
}
return;
}
}
}
void BFS(void)
{
int operation[1000]={0}; //当前步的操作: 1z0:清空z瓶子 2z0:装满z瓶子 3xy:从x瓶倒向y瓶
map<string,bool>vist;
vist["0,0"]=true;
process queue[1000]; //状态队列
int head,tail;
queue[head=0].x=0;
queue[tail=0].y=0;
queue[tail++].step=0;
string ts; //temporary
while(head<tail)
{
process p=queue[head];
if(p.x==c || p.y==c) //得到要求的剩余水量c
{
cout<<p.step<<endl;
/*下标回溯,输出操作过程*/
int ps=p.step;
int* steps=new int[ps+1]; //从1到p.step顺序记录各步操作的下标,不使用steps[0]
steps[ps--]=tail-1;
while(ps)
{
steps[ps]=queue[ steps[ps+1] ].pos;
ps--;
}
for(int i=1;i<=p.step;i++)
{
int temp=operation[ steps[i]-1 ]; //注意各个数组间的下标关系
switch(temp/100)
{
case 1:
{
cout<<"DROP("<<(temp/10)%10<<')'<<endl;
break;
}
case 2:
{
cout<<"FILL("<<(temp/10)%10<<')'<<endl;
break;
}
case 3:
{
cout<<"POUR("<<(temp/10)%10<<','<<temp%10<<')'<<endl;
break;
}
}
}
delete steps;
return;
}
/*装满v1*/
k1=p.x;
k2=p.y;
fill(1);
ts=combAB(k1,k2);
if(!vist[ts])
{
vist[ts]=true;
queue[tail].x=k1;
queue[tail].y=k2;
queue[tail].step=p.step+1; //当前的操作步数
queue[tail].pos=head; //前一步操作在queue[]中的下标
operation[tail++]=210; //当前的操作
}
/*装满v2*/
k1=p.x;
k2=p.y;
fill(2);
ts=combAB(k1,k2);
if(!vist[ts])
{
vist[ts]=true;
queue[tail].x=k1;
queue[tail].y=k2;
queue[tail].step=p.step+1;
queue[tail].pos=head;
operation[tail++]=220;
}
/*清空v1*/
k1=p.x;
k2=p.y;
drop(1);
ts=combAB(k1,k2);
if(!vist[ts])
{
vist[ts]=true;
queue[tail].x=k1;
queue[tail].y=k2;
queue[tail].step=p.step+1;
queue[tail].pos=head;
operation[tail++]=110;
}
/*清空v2*/
k1=p.x;
k2=p.y;
drop(2);
ts=combAB(k1,k2);
if(!vist[ts])
{
vist[ts]=true;
queue[tail].x=k1;
queue[tail].y=k2;
queue[tail].step=p.step+1;
queue[tail].pos=head;
operation[tail++]=120;
}
/*v1倒向v2*/
k1=p.x;
k2=p.y;
pour(1,2);
ts=combAB(k1,k2);
if(!vist[ts])
{
vist[ts]=true;
queue[tail].x=k1;
queue[tail].y=k2;
queue[tail].step=p.step+1;
queue[tail].pos=head;
operation[tail++]=312;
}
/*v2倒向v1*/
k1=p.x;
k2=p.y;
pour(2,1);
ts=combAB(k1,k2);
if(!vist[ts])
{
vist[ts]=true;
queue[tail].x=k1;
queue[tail].y=k2;
queue[tail].step=p.step+1;
queue[tail].pos=head;
operation[tail++]=321;
}
head++;
}
cout<<"impossible"<<endl;
return;
}
int main(void)
{
while(cin>>v1>>v2>>c)
BFS();
return 0;
}



