- POJ 3252 - Round Numbers
- Time: 2000MS
- Memory: 65536K
- 难度: 初级
- 分类: 排列组合
问题描述
输入两个十进制正整数a和b,求闭区间 [a ,b] 内有多少个 Round number
所谓的 Round Number 就是把一个十进制数转换为一个无符号二进制数,若该二进制数中0的个数大于等于1的个数,则它就是一个Round Number
注意:
- 转换所得的二进制数,最高位必然是1,最高位的前面不允许有0
-规定输入范围:1 <= a < b <= 2E
解题思路
很猥琐的题,我首先说说猥琐的地方,再说说解题思路,有四点很猥琐:
- (1)规定输入范围:
1 <= a < b <= 2E
输入的数是一个接近大数的非大数, int可以存储。网上看很多同学都说要用到精度,其实完全没必要,int能表示21E+的整数,精确的int极限能表示的正整数为2147483647,但是即使这样,面对这题也不能松懈啊!bin[]边界的最小值为 35 !! - (2)
bin[]数组若果定义为局部数组,等着WA吧!
我找不到任何原因为什么会这样,bin不管是全局定义 还是 局部定义,本地是完全AC的,上传就出问题了,局部WA,全局AC。
我被迫把传参del掉,把bin改为全局,郁闷! - (3)组合数打表,同(1)的猥琐,
c[][]边界的最小值为33,就是说如果定义组合表的大小比c[33][33]小的,就等着RE吧!
还有就是这个算法有一个违背常识的处理,要把c[0][0]=1,不然某些最终结果会少1 - (4)输入不能用循环输入
while(cin>>…),不然你就等着OLE (就是Output Limit Excessed,很少见吧!)。不知道数据库是怎么回事,输入竟然不会根据读取数据结束而结束,而是无限输出最后一次输入所得的结果……老老实实一次输出就end file吧!
组合数学题,(也属 递推数学,是因为杨辉三角和组合数之间的关系)
我根据我写的程序讲解好了。
要知道闭区间 [a ,b] 内有多少个Round number,只需要分别求出:
- 闭区间
[0, a]内有T个RN - 闭区间
[0, b+1]内有S个RN - 再用
S – T就是闭区间[a, b]内的RN数了
至于为什么是
b+1,因为对于闭区间[0, k],我下面要说的算法求出的是比k小的RN数,就是说不管 k是不是RN, 都没有被计算在内,所以若要把闭区间[a, b]的边界a和b都计算在内,就要用上述的处理方法。
现在问题的关键就是如何求 [0, k] 内的RN数了:
首先要把k转化为二进制数 bin-k ,并记录其位数(长度)len
那么首先计算长度小于len的RN数有多少(由于这些数长度小于len,那么他们的值一定小于k,因此在进行组合时就无需考虑组合所得的数与k之间的大小了)
for(i=1;i<bin[0]-1;i++) //bin[0]记录的是二进制数的长度len
for(j=i/2+1;j<=i;j++)
sum+=c[i][j];可以看到,i<len-1,之所以减1,是因为这些长度比len小的数,最高位一定是1,那么剩下可供放入数字的位数就要再减少一个了。
这条程序得到的sum为
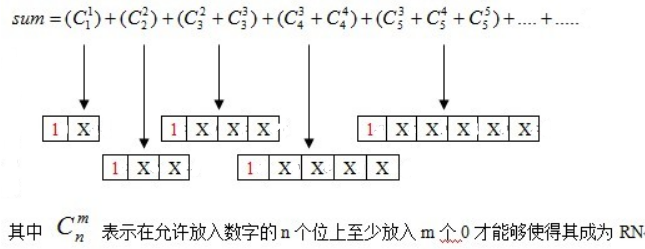
1表示当前处理的二进制数的最高位,X表示该二进制数待放入数字的位。
显然这段程序把 二进制数0 排除在外了,这个是最终结果没有影响的,因为最后要把区间 [a, b] 首尾相减,0存不存在都一样了。
然后计算长度等于len的RN数有多少(由于这些数长度等于len,那么他们的值可能小于k,可能大于k,因此在进行组合时就要考虑组合所得的数与k之间的大小了)
int zero=0; //从高位向低位搜索过程中出现0的位的个数
for(i=bin[0]-1;i>=1;i--)
if(bin[i]) //当前位为1
for(j=(bin[0]+1)/2-(zero+1);j<=i-1;j++)
sum+=c[i-1][j];
else
zero++;之所以初始化 i=bin[0]-1 ,是因为 bin[] 是逆向存放k的二进制的,因此要从高位向低位搜索,就要从 bin[] 后面开始,而要 bin[0]-1 ,是因为默认以后组合的数长度为len,且最高位为1,因此最高位不再搜索了。
现在问题的关键就是怎样使得以后组合的数小于k了
这个很简单:
从高位到低位搜索过程中,遇到当前位为0,则不处理,但要用计数器zero累计当前0出现的次数
遇到当前位为1,则先把它看做为0,zero+1,那么此时当前位 后面的 所有低位任意组合都会比k小,找出这些组合中RN的个数,统计完毕后把当前位恢复为原来的1,然后 zero-1,继续向低位搜索。
剩下的问题就是 当当前位为1时,把它看做0之后,怎样去组合后面的数了
此时组合要考虑2个方面:
(1)当前位置i后面允许组合的低位有多少个,我的程序由于bin是从
bin[1]开始存储二进制数的,因此 当前位置i后面允许组合的低位有i-1个(2) 组合前必须要除去前面已出现的0的个数zero
我的程序中初始化 j=(bin[0]+1)/2-(zero+1), j本来初始化为 (bin[0]+1)/2 就可以了,表示对于长度为 bin[0] 的二进制数,当其长度为偶数时,至少其长度一半的位数为0,它才是RN,当其长度为奇数时,至少其长度一半+1的位数为0,它才是RN。
但是现在还必须考虑前面出现了多少个0,根据前面出现的0的个数,j的至少取值会相应地减少。 -(zero+1) ,之所以 +1,是因为要把当前位 bin[i] 看做0
然后到了最后,剩下一个问题就是怎样得到每一个 的值,这个我发现很多同学都是利用打表做的,利用的就是 组合数 与 杨辉三角 的关系(建立一个二维数组 C[n], 就能看到他们之间关系密切啊!区别就是顶点的值,杨辉三角为1,组合数为0)
其实这个“关系”是有数学公式的:
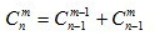
好好体会一下吧!
其实组合数也可以直接用计算方法做(n的规模可以至少扩展到1000),不过这里n的规模只有26,打表应该是更快的,有兴趣学习用计算方法做组合数的同学可以联系我,这个要用另外的数学方法处理。
AC 源码
//Memory Time
//224K 16MS
#include<iostream>
using namespace std;
int c[33][33]={0};
int bin[35]; //十进制n的二进制数
/*打表,计算nCm*/
void play_table(void)
{
for(int i=0;i<=32;i++)
for(int j=0;j<=i;j++)
if(!j || i==j)
c[i][j]=1;
else
c[i][j]=c[i-1][j-1]+c[i-1][j];
// c[0][0]=0;
return;
}
/*十进制n转换二进制,逆序存放到bin[]*/
void dec_to_bin(int n)
{
bin[0]=0; //b[0]是二进制数的长度
while(n)
{
bin[++bin[0]]=n%2;
n/=2;
}
return;
}
/*计算比十进制数n小的所有RN数*/
int round(int n)
{
int i,j;
int sum=0; //比十进制数n小的所有RN数
dec_to_bin(n);
/*计算长度小于bin[0]的所有二进制数中RN的个数*/
for(i=1;i<bin[0]-1;i++)
for(j=i/2+1;j<=i;j++)
sum+=c[i][j];
/*计算长度等于bin[0]的所有二进制数中RN的个数*/
int zero=0; //从高位向低位搜索过程中出现0的位的个数
for(i=bin[0]-1;i>=1;i--)
if(bin[i]) //当前位为1
for(j=(bin[0]+1)/2-(zero+1);j<=i-1;j++)
sum+=c[i-1][j];
else
zero++;
return sum;
}
int main(void)
{
play_table();
int a,b;
cin>>a>>b;
cout<<round(b+1)-round(a)<<endl;
return 0;
}



