- POJ 3083 - Children of the Candy Corn
- Time: 1000MS
- Memory: 65536K
- 难度: 初级
- 分类: DFS
问题描述
给定一个迷宫,S是起点,E是终点,# 是墙不可走,. 可以走
先输出左转优先时,从S到E的步数
再输出右转优先时,从S到E的步数
最后输出S到E的最短步数
W为宽,列数
H为高,行数
解题思路
DFS和BFS的综合题水题,难度不大,但是写代码时要注意几方面:
1、 左转、右转优先搜索时必须标记当前位置时的方向,我定义的方向是
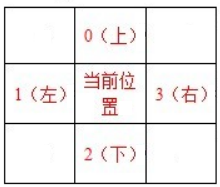
最初的方向由起点S确定,而下一步的方向则由前一步的走向决定。
例如 左边优先搜索:
当前位置的方向指向 1(向左),(这同时说明前一步是在第“3”的位置走过来的)
那么走下一步时,就要根据2103的顺序,先逐格确定当前位置周边的四格是否可行
若第一次确认2可行,就走到2,在位置2时的方向为2(向下)
若2不可行,则再确定1,若1可行,就走到1,在位置1时的方向为1(向左)
若1也不可行,则再确定0,若0可行,就走到0,在位置0时的方向为0(向上)
若0也不可行,说明进入了迷宫的死胡同,要从原路返回,走回3
右边优先搜索也同理。
根据我定义的方向,设当前位置为d,那么:
- 左转,用数学式子表达就是
d=(d+1)%4 - 右转,用数学式子表达就是
d=(d+3)%4
我比较懒,在我的程序中,DFS和BFS都用了多入口的做法,有兴趣的同学可以利用我给出的这两个式子对代码进行优化。
这里还有一点必须要注意的: 左边、右边优先搜索都不是找最短路,因此走过的路可以再走,无需标记走过的格
2、寻找最短路只能用BFS
因此在做第3问时别傻乎乎的又用DFS,DFS对于样例的输入确实和BFS得到的结果一样的,别以为样例PASS就提交了。。。所以我就说样例没代表性,学会测试数据很重要= =
需要注意的还有:
- 要求E的最短路,必须把迷宫模拟为树,S为根,找到E所在的层(树深),该层就是S到E的最短路,处理技巧就是在BFS时,令
queue[tail]的depth等于对应的queue[head]的depth+1,详细见我的程序 - 把循环的次数作为深度就铁定错的
AC 源码
//Memory Time
// 212K 0MS
#include<iostream>
using namespace std;
typedef class
{
public:
int r,c;
int depth;
}SE;
SE s,e; //起止点
int Lstep; //左边优先搜索 时从S到E的总步数
int Rstep; //右边优先搜索 时从S到E的总步数
int shortstep; //S到E的最少总步数
bool maze[41][41]; //记录迷宫的“可行域”与“墙”
void DFS_LF(int i,int j,int d) //左边优先搜索,i,j为当前点坐标,d为当前位置方向
{
Lstep++;
if(i==e.r && j==e.c)
return;
switch(d)
{
case 0:
{
if(maze[i][j-1])
DFS_LF(i,j-1,1);
else if(maze[i-1][j])
DFS_LF(i-1,j,0);
else if(maze[i][j+1])
DFS_LF(i,j+1,3);
else if(maze[i+1][j])
DFS_LF(i+1,j,2);
break;
}
case 1:
{
if(maze[i+1][j])
DFS_LF(i+1,j,2);
else if(maze[i][j-1])
DFS_LF(i,j-1,1);
else if(maze[i-1][j])
DFS_LF(i-1,j,0);
else if(maze[i][j+1])
DFS_LF(i,j+1,3);
break;
}
case 2:
{
if(maze[i][j+1])
DFS_LF(i,j+1,3);
else if(maze[i+1][j])
DFS_LF(i+1,j,2);
else if(maze[i][j-1])
DFS_LF(i,j-1,1);
else if(maze[i-1][j])
DFS_LF(i-1,j,0);
break;
}
case 3:
{
if(maze[i-1][j])
DFS_LF(i-1,j,0);
else if(maze[i][j+1])
DFS_LF(i,j+1,3);
else if(maze[i+1][j])
DFS_LF(i+1,j,2);
else if(maze[i][j-1])
DFS_LF(i,j-1,1);
break;
}
}
return;
}
void DFS_RF(int i,int j,int d) //右边优先搜索,i,j为当前点坐标,d为当前位置方向
{
Rstep++;
if(i==e.r && j==e.c)
return;
switch(d)
{
case 0:
{
if(maze[i][j+1])
DFS_RF(i,j+1,3);
else if(maze[i-1][j])
DFS_RF(i-1,j,0);
else if(maze[i][j-1])
DFS_RF(i,j-1,1);
else if(maze[i+1][j])
DFS_RF(i+1,j,2);
break;
}
case 1:
{
if(maze[i-1][j])
DFS_RF(i-1,j,0);
else if(maze[i][j-1])
DFS_RF(i,j-1,1);
else if(maze[i+1][j])
DFS_RF(i+1,j,2);
else if(maze[i][j+1])
DFS_RF(i,j+1,3);
break;
}
case 2:
{
if(maze[i][j-1])
DFS_RF(i,j-1,1);
else if(maze[i+1][j])
DFS_RF(i+1,j,2);
else if(maze[i][j+1])
DFS_RF(i,j+1,3);
else if(maze[i-1][j])
DFS_RF(i-1,j,0);
break;
}
case 3:
{
if(maze[i+1][j])
DFS_RF(i+1,j,2);
else if(maze[i][j+1])
DFS_RF(i,j+1,3);
else if(maze[i-1][j])
DFS_RF(i-1,j,0);
else if(maze[i][j-1])
DFS_RF(i,j-1,1);
break;
}
}
return;
}
void BFS_MSS(int i,int j) //最短路搜索
{
bool vist[41][41]={false};
SE queue[1600];
int head,tail;
queue[head=0].r=i;
queue[tail=0].c=j;
queue[tail++].depth=1; //当前树深标记,这是寻找最短路的关键点
vist[i][j]=true;
while(head<tail)
{
SE x=queue[head++];
if(x.r==e.r && x.c==e.c)
{
cout<<x.depth<<endl;
return;
}
if(maze[x.r][x.c-1] && !vist[x.r][x.c-1])
{
vist[x.r][x.c-1]=true;
queue[tail].r=x.r;
queue[tail].c=x.c-1;
queue[tail++].depth=x.depth+1;
}
if(maze[x.r-1][x.c] && !vist[x.r-1][x.c])
{
vist[x.r-1][x.c]=true;
queue[tail].r=x.r-1;
queue[tail].c=x.c;
queue[tail++].depth=x.depth+1;
}
if(maze[x.r][x.c+1] && !vist[x.r][x.c+1])
{
vist[x.r][x.c+1]=true;
queue[tail].r=x.r;
queue[tail].c=x.c+1;
queue[tail++].depth=x.depth+1;
}
if(maze[x.r+1][x.c] && !vist[x.r+1][x.c])
{
vist[x.r+1][x.c]=true;
queue[tail].r=x.r+1;
queue[tail].c=x.c;
queue[tail++].depth=x.depth+1;
}
}
return;
}
int main(int i,int j)
{
int test;
cin>>test;
while(test--)
{
int direction; //起点S的初始方向
int w,h; //size of maze
cin>>w>>h;
/*Initial*/
Lstep=1;
Rstep=1;
memset(maze,false,sizeof(maze));
/*Structure the Maze*/
for(i=1;i<=h;i++)
for(j=1;j<=w;j++)
{
char temp;
cin>>temp;
if(temp=='.')
maze[i][j]=true;
if(temp=='S')
{
maze[i][j]=true;
s.r=i;
s.c=j;
if(i==h)
direction=0;
else if(j==w)
direction=1;
else if(i==1)
direction=2;
else if(j==1)
direction=3;
}
if(temp=='E')
{
maze[i][j]=true;
e.r=i;
e.c=j;
}
}
/*Left First Search*/
switch(direction)
{
case 0: {DFS_LF(s.r-1,s.c,0); break;}
case 1: {DFS_LF(s.r,s.c-1,1); break;}
case 2: {DFS_LF(s.r+1,s.c,2); break;}
case 3: {DFS_LF(s.r,s.c+1,3); break;}
}
cout<<Lstep<<' ';
/*Right First Search*/
switch(direction)
{
case 0: {DFS_RF(s.r-1,s.c,0); break;}
case 1: {DFS_RF(s.r,s.c-1,1); break;}
case 2: {DFS_RF(s.r+1,s.c,2); break;}
case 3: {DFS_RF(s.r,s.c+1,3); break;}
}
cout<<Rstep<<' ';
/*Most Short Step Search*/
BFS_MSS(s.r,s.c);
}
return 0;
}



