- POJ 1009 - Edge Detection
- Time: 1000MS
- Memory: 10000K
- 难度: 中级
- 分类: 模拟法
问题描述
某种卫星使用一种叫做 run length encoding 的方式来储存大尺寸图片,
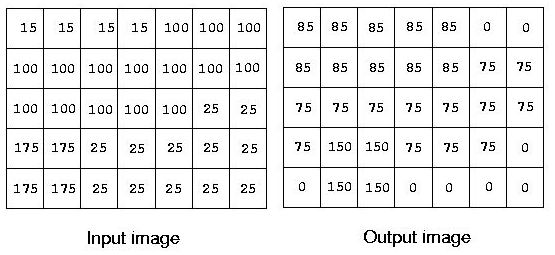
有一种简单的 edge detection 算法是将图像中的每一个点的值与他周围的八个点相减,然后记录下绝对值最大的,上面的右图是左图经过这种算法转换之后的结果。
现在你的任务就是实现这个算法,输入的图片是以 run length encoding 的形式表示的,同时也要求转换后的图片也以 run length encoding 的形式表示。
解题思路
非常令人纠结的模拟题:
- 由于图片宽度可能为
10^9,因此不能开数组,会 MLE - 又因为像素点很多,不能直接暴力,会 TLE
突破点在于 Input 的 pair,pair 上限只有 1000,数据量是最少的,因此只能利用这点去解题。
要利用 pair,就必须懂得 “跳跃式编码”,就是说只在像素发生变化的位置进行编码,而像素没有变化的位置则其编码值与其左边的像素一致。
我只说解题方法,不给证明了。
先给所有像素点 pix 顺序标号 pos,从 1 开始,以这个标号 pos 作为该像素点 pix 的索引,
利用 pos 去模拟 pix 在二维图片的坐标:
row = (pos-1) / widthcol = (pos-1) % width
这样就无需定义二维数组,仅仅虚构了一个二维数组,就解决了空间溢出 MLE 的问题。
接下来在 像素发生变化的位置(下面称为“边界”)的地方编码,
边界位置其实就是每对 pair 的个数决定的,对边界位置及其周遭共 9 个像素点编码,把编码结果及对应的索引 pos 都存放在 OutMap,编码方法就是题目给出的算法。
最后把 OutMap 中的编码值根据其索引值进行升序排序,依次读取 OutMap 中的编码值,当编码值 code 发生变化时,则用 变化后的编码索引 减去 变化前的编码索引,就是 code 在 OutMap 中出现的次数。
测试数据
- 来源(已失效):Mid-Central USA 2000
- 输入:input
- 输出:output
AC 源码
//Memory Time
//332K 32MS
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int size=1000; //每幅图片的pair上限
int width; //Map的宽
int total=0; //像素点总个数
typedef class OutMapPix
{
public:
int pos; //OutMap中每个像素点的顺序位置,pos从1开始
int code; //OutMap中每个像素点对应InMap的编码
}Pix;
int InMapPair[size][2]; //InMapPair[][0]为像素值,InMapPair[][1]为InMapPair[][0]连续出现的个数
Pix OutMap[size*8]; //每个pix都依赖其周围的8个点编码
int cmp(const void* a,const void* b); //快排比较规则
int GetValue(int pos); //返回第pos个像素点的像素值
int GetCode(int pos); //返回第pos个像素点的编码
int main(int k)
{
while(cin>>width && width)
{
int pairv,pairt;
k=total=0;
while(cin>>pairv>>pairt && pairt)
{
InMapPair[k][0]=pairv;
InMapPair[k++][1]=pairt;
total+=pairt;
}
int PairNum=k; //pair的个数
cout<<width<<endl;
int pos=1; //当前处理的像素点的位置
k=0; //OutMap[]指针
for(int p=0;p<=PairNum;p++)
{
int row=(pos-1)/width; //得到pos在二维图对应的坐标
int col=(pos-1)%width;
for(int i=row-1;i<=row+1;i++) //枚举(row,col)周围及其自身共9个点(x,y)
for(int j=col-1;j<=col+1;j++)
{
int tpos=i*width+j; //得到(x,y)的顺序位置
if(i<0 || j<0 || j>=width || tpos>=total)
continue;
OutMap[k].pos=tpos+1;
OutMap[k++].code=GetCode(tpos+1); //对发生变化的像素点的附近8个点编码
}
pos+=InMapPair[p][1]; //跳跃,确定下一个像素发生变化的点的位置
}
qsort(OutMap,k,sizeof(Pix),cmp); //对OutMap根据顺序位置
/*OutPut*/
Pix temp=OutMap[0];
for(int i=0;i<k;i++)
{
if(temp.code==OutMap[i].code)
continue;
cout<<temp.code<<' '<<OutMap[i].pos-temp.pos<<endl;
temp=OutMap[i];
}
cout<<temp.code<<' '<<total-temp.pos+1<<endl;
cout<<"0 0"<<endl;
}
cout<<0<<endl;
return 0;
}
/*快排比较规则*/
int cmp(const void* a,const void* b)
{
Pix* x=(Pix*)a;
Pix* y=(Pix*)b;
return x->pos - y->pos;
}
/*返回第pos个像素点的像素值*/
int GetValue(int pos)
{
int i=0,p=0;
while(p<pos)
p+=InMapPair[i++][1];
return InMapPair[i-1][0];
}
/*返回第pos个像素点的编码*/
int GetCode(int pos)
{
int code=GetValue(pos);
int MaxAbs=0;
int row=(pos-1)/width;
int col=(pos-1)%width;
for(int i=row-1;i<=row+1;i++)
for(int j=col-1;j<=col+1;j++)
{
int tpos=i*width+j;
if(i<0 || j<0 || j>=width || tpos>=total || tpos==pos-1) //tpos==pos-1为中心的像素点,即当前待编码的点
continue;
int tcode=GetValue(tpos+1);
if(MaxAbs<abs(tcode-code)) //注意取绝对值
MaxAbs=abs(tcode-code);
}
return MaxAbs;
}



